PAT1053.Path of Equal Weight

Jul 17, 2019

题目

Given a non-empty tree with root R, and with weight W**i assigned to each tree node T**i. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.

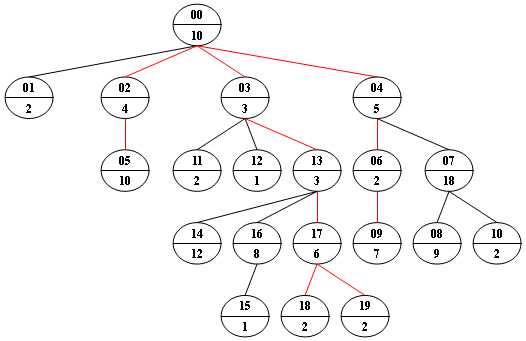
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let’s consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0<N≤100, the number of nodes in a tree, M (<N), the number of non-leaf nodes, and 0<S<230, the given weight number. The next line contains N positive numbers where W**i (<1000) corresponds to the tree node T**i. Then M lines follow, each in the format:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID’s of its children. For the sake of simplicity, let us fix the root ID to be 00.

Output Specification:

For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.

Note: sequence {A1,A2,⋯,A**n} is said to be greater than sequence {B1,B2,⋯,B**m} if there exists 1≤k<min{n,m} such that A**i=B**i for i=1,⋯,k, and A**k+1>B**k+1.

Sample Input:

20 9 24
10 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 2
00 4 01 02 03 04
02 1 05
04 2 06 07
03 3 11 12 13
06 1 09
07 2 08 10
16 1 15
13 3 14 16 17
17 2 18 19

Sample Output:

Special thanks to Zhang Yuan and Yang Han for their contribution to the judge’s data.

代码

#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
struct node{
    int weight;
    vector<int> child;
}Node[105];


bool cmp(const int &a,const int &b)
{
    return Node[a].weight>Node[b].weight;
}

int n,m,s;
vector<int> way;

void dfs(int id,int now)
{
    now+=Node[id].weight;
    way.push_back(Node[id].weight);

    if(now>s)
    {
        way.pop_back();
        return ;
    }

    if(now==s&&Node[id].child.empty())
    {
        for(vector<int>::iterator it=way.begin();it!=way.end();it++)
        {
            printf("%d",*it);
            if(it!=way.end()-1)
                printf(" ");
            if(it==way.end()-1)
                printf("\n");
        }
    }

    for(vector<int>::iterator it=Node[id].child.begin();
            it!=Node[id].child.end();it++)
        {
            dfs(*it,now);
        }

    way.pop_back();
    return ;
}
int main()
{

    scanf("%d%d%d",&n,&m,&s);
    for(int i=0;i<n;i++)
        scanf("%d",&Node[i].weight);
    for(int i=0;i<m;i++)
    {
        int id,num,tmp;
        scanf("%d%d",&id,&num);
        for(int j=0;j<num;j++)
        {
            scanf("%d",&tmp);
            Node[id].child.push_back(tmp);
        }
        sort(Node[id].child.begin(),Node[id].child.end(),cmp);


    }
    dfs(0,0);
    return 0;
}

分析

对树进行DFS遍历，now为当前路径权重，当权重等于题目给的s时若已经到达叶子节点则输出该条路径。

sort函数默认从小到大排序，从大到小排序的写法：

bool cmp(const int &a,const int &b) { return Node[a].weight>Node[b].weight; }

注意是对节点权重的比较而不是节点号的比较。

error: 'vector' does not name a type

是因为没有 using namespace std;